The (Almost) Impossible Chessboard Problem

The Problem Commentary Solution Play

Solution
<
Binary Numbers
We need to know how to represent decimal numbers in binary and vice-versa. Our ordinary (decimal) numbers are base-10. This means that the rightmost digit tells as how many ones (100) there are, the next tells us how many tens (101), the next how many 100's (102) and so on. For example, the number 567 is the sum of 5 100's, 6 tens and 7 ones (5 * 102 + 6 * 101 + 7 * 100).
A binary number is base-2. This means that the rightmost digit tells as how many ones (20) there are, the next tells us how many 2's (21), the next how many 4's (22) and so on. Note that, while there are 10 decimal digits (0-9), there are only 2 binary digits (0 and 1). Binary digits are commonly called bits. We will be working with 6-bit binary numbers for this puzzle. Here are some examples:
  • 000001 = 0 * 25 + 0 * 24 + 0 * 23 + 0 * 22 + 0 * 21 + 1 * 20 = 1 base10
  • 000111 = 0 * 25 + 0 * 24 + 0 * 23 + 1 * 22 + 1 * 21 + 1 * 20 = 4 + 2 + 1 = 7 base10
  • 101010 = 1 * 25 + 0 * 24 + 1 * 23 + 0 * 22 + 1 * 21 + 0 * 20 = 32 + 8 + 2 = 42 base10
  • 111111 = 1 * 25 + 1 * 24 + 1 * 23 + 1 * 22 + 1 * 21 + 1 * 20 = 32 + 16 + 8 + 4 + 2 + 1 = 63 base10
With 6 bits, we can represent 64 different numbers (0-63 in decimal). Not coincidently, this allows us to associate a unique binary number with each square of the board.
We need to be comfortable going back and forth between decimal and binary in order to continue. If I haven't explained it well enough, there are many resources on the Internet.
Calculating the Value of the Board
We're now going to learn an algorithm (series of steps) which produces a 6 bit number, which we call the value, from a checkerboard with heads and tails. To begin, we number the squares of the board from 0 to 63 starting in the upper left corner and ending in the lower right.
We're going to examine 6 groups of squares and, for each group, determine whether the number of heads is odd or even. (We say that a group of squares with an odd number of heads is odd parity and a group with an even number of heads is even parity.) Each group will give us one of the six bits in the value.
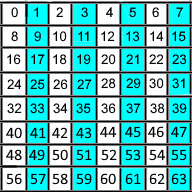
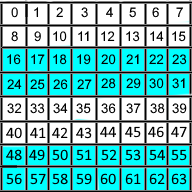
The first group is the even-numbered columns (2, 4, 6, 8) as shown in Figure 1. If the group is even-parity (the number of heads in the group is even), we set the "ones bit" of the value to 0. If the group has odd parity, we set the "ones bit" of the value to 1.
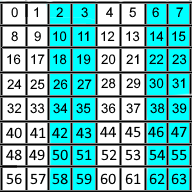
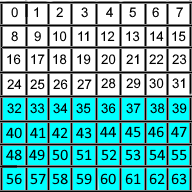
The second group is the 4 columns (3, 4, 7, 8) as shown in Figure 2. If the group has even parity, we set the "2's bit" of the value to 0. If the group has odd parity, we set the "2's bit" of the value to 1.
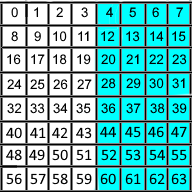
The third group is the 4 rightmost columns (5, 6, 7, 8) as shown in Figure 3. This group gives us the "4's bit" of the value. Even parity = 0, odd = 1;
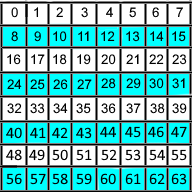
The fourth group is the even-numbered rows (2, 4, 6, 8) as shown in Figure 4. This group gives us the "8's bit" of the value. Even parity = 0, odd = 1;
The fifth group is the 4 rows (3, 4, 7, 8) as shown in Figure 5. This group gives us the "16's bit" of the value. Even parity = 0, odd = 1;
Finally, the sixth group is the 4 bottom-most rows (5, 6, 7, 8) as shown in Figure 6. This group gives us the "32's bit" of the value. Even parity = 0, odd = 1;
We now have a 6 bit number, the value of this board. Converted to decimal, this value is a number between 0 and 63 which we can use to reference a certain square of the board.
Figure 1
Figure 2
Figure 3
Figure 4
Figure 5
Figure 6
Your Friend's Job
When your friend comes into the room, he simply calculates the value of the board, converts it to decimal and guesses that square. You can practice this by clicking Play above. Once you have your guess, click Find the Key and see if you're correct.
Your Job
Your job as the flipper is a bit more complicated. Calculate the value and write it down. Beneath it, write the 6 bit number that specifies the square with the key. Exclusive-or* these two numbers. Convert this to decimal and flip the corresponding square. You can practice this procedure by clicking the Play button above.

* Exclusive-Or is like adding without carry. In a column, the result bit is 0 if the two bits being added are both 0 or both 1. The result bit is 1 if one of the bits being added is 1 and the other is 0. One or the other but not both. 1 + 1 = 0. 1 + 0 = 1. 0 + 0 = 0. 0 + 1 = 1.